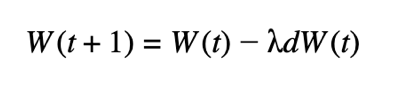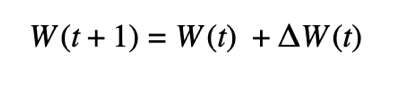An Edgify Research Team Publication
This is the first, introductory post, in our three part algorithmic series on real-world distributed training on the edge. In it, we present and compare the two fundamental methods for this type of machine learning (and Deep Learning in particular). The post following this one will then address communication compression, and the final one will attend to the challenge that non-IID distributions pose, specifically for Batch Normalization.
Distributed Edge Training
With the increased penetration and proliferation of IoT devices, and the continuous increase in connected, everyday devices (from smartphones to cars to self check out stands), the amount of data collected from the world is increasing exponentially. Against this, there are:
- Growing privacy concerns, and the security risks associated with access to so much data.
- Costs or constraints on transmitting all that data for training purposes.
A question presents itself: With all of the data generated on these edge devices, and with those devices having more processing power than ever before — does the data really need to leave the device? Why not just have the training process itself run on the edge device? This, to be sure, goes well beyond the commonly used term “AI at the edge”, which usually refers to the use of local models (that merely make predictions on the device).

Now, a single edge device still offers a highly limited amount of collected data and packs relatively little computational power. But in many contexts there is a multitude of them that are performing very similar training tasks. If these could all collaborate between them, and together train a shared model, one that gains from the vast data collected from all of them, it would be a whole new ball game. And if this could be done while keeping the data on the devices themselves (as they are the ones who carry out the training anyway), it would decouple the ability to train the shared model from the need to store the data in a datacenter.
This would be nothing short of a revolution for AI privacy.

A new generation of algorithms for training deep learning models, that do just that, is emerging. This is what we term Distributed Edge Training, bringing the model’s training process to the edge device, while collaborating between the various devices to reach an optimized model. For a more product/solution- oriented overview, see our initial post on the topic. Here, we attend to the algorithmic core of these methods.
The Basic Idea and Its Challenges
Our goal is to train a high-quality model while the training data remains distributed over a large number of edge devices. This is done as follows:
The instances of learning algorithms running on the edge devices, all rely on a shared model for their training. In a series of rounds, each device, after downloading the current model (or what it takes to deduce it), independently computes some form of update to that model based on its local data. It communicates this update back to the server, where the updates are then aggregated to compute a new global model. During the process, the training data remains on the edge devices.
We will explore and compare two of the most common approaches for powering Distributed Edge Training: Federated Learning (as promoted first and foremost by Google) and Large Batch Learning (see also here) (by Facebook and others) {originally suggested for fast training on hyper computing clusters.}
Though the idea behind Distributed Edge Training is conceptually simple, it can get technically complex. These approaches are efficient in some scenarios, but have proven to be much more challenging in others, depending on various factors:
- The number of concurrent edge devices that impact the shared model (where a large number of endpoints can hinder performance)
- The distribution of data among those endpoints (where an uneven, non IID fashion presents a deep challenge to such approaches)
- Network bandwidth limitations (where not all approaches lend themselves to compression schemes equally)
We have set out to evaluate Federated Learning and Large Batch with respect to these factors and others. The next two posts, specifically, will revolve around points 2 and 3 respectively.

For presentation’s sake, we will be making a number of simplifying assumptions:
- All communication between the edge devices is done through a single, central server.
- Synchronised Algorithms — a simple implementation of the distribution framework. It requires that each device sends a model or model gradients (or model update) back to the server during each round.
- The Machine Learning algorithmic framework is that of Deep Learning (other methods also lend themselves to such distribution schemes).
- Furthermore, the Deep Learning training uses a standard optimizer — Stochastic Gradient Descent (SGD).
Large Batch
In classical, non-distributed batch training, a batch of samples is used in order to perform a stochastic gradient descent optimization step. With large batches allowed for (With large batches allowed for — which is not always simple or even feasible), it is rather straightforward for this process to be a distributed one, running over many server GPUs or, in our case, edge devices:
While each edge device has its own local data, that can be considered as part of the batch. Each device, performing a forward and backward pass on its data, calculates a single local gradient each time. The calculated gradient is then sent to the server, where these are all aggregated, for the sake of a global update to the model. (The aggregate or the updated model are sent back to the devices, and the cycle repeats.)
To spell out the Large Batch steps:
- Initialise the weights for the shared model.
— — — — — — — — edge device phase — — — — — — — — - Download the current shared model.
- Run a single pass of forward prediction and backward error propagation.
- Compress the gradients.
- Upload the update to a central server.
— — — — — — — — server phase — — — — — — — — - Decompress the incoming gradients and compute their average
- Perform a single step of SGD to update the shared model.
- Go to step 2 (edge training phase).
Federated Learning
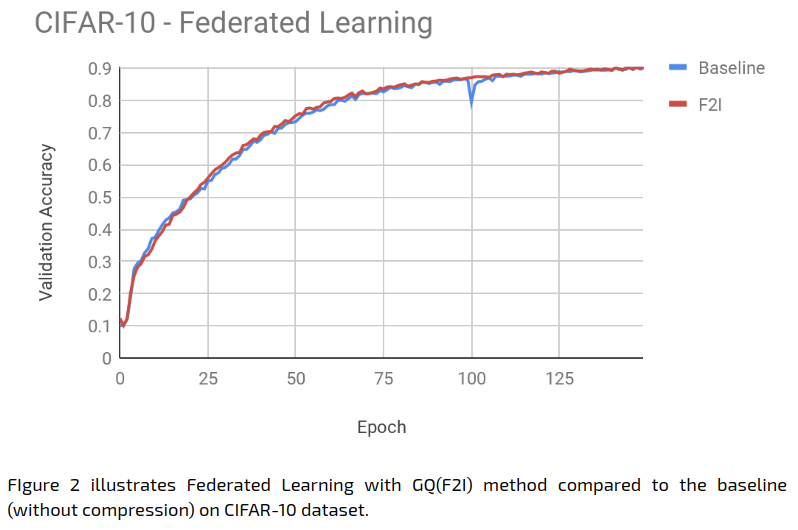
In Large Batch, in every round, each device performs a single forward-backward pass, and immediately communicates the gradient. In Federated Learning, in contrast, in every round, each edge device performs some independent training on its local data (that is, without communicating with the other devices), for several iterations. Only then does it send its model-update to the server to be aggregated with those of the other devices, for the sake of an improved shared model (from which this process can then repeat).
Here, too, during the whole process, all of the training data remains on the devices.
To spell out the Federated Learning steps:
- Initialise the weights for the shared model.
— — — — — — — — edge device phase — — — — — — — — - Download the current shared model.
- Run a number of SGD iterations (based on forward and backward passes upon the local data).
- Compress the updated model weights (optional).
- Upload the update to the central server.
— — — — — — — — server phase — — — — — — — — - Decompress the incoming weights of the machines’ models if needed.
- Compute their average.
- Update the shared model.
- Go to step 2 (edge training phase).
The Two Approaches in Comparison

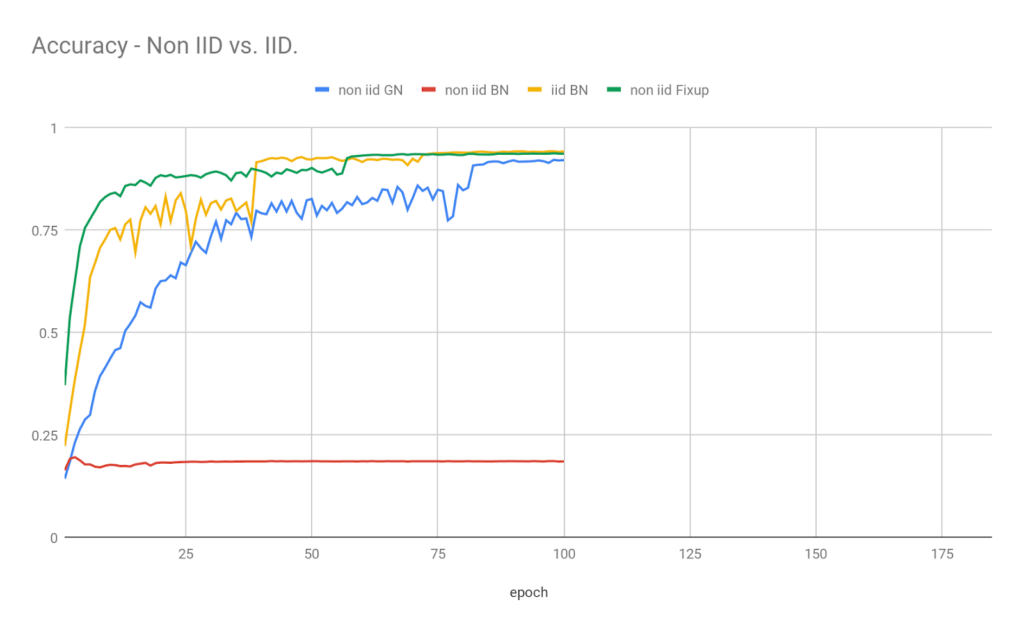
Without the multi-stage device independent training of Federated Learning, distributed Large Batch training is more similar to classical training, in which the data resides in one central location. The average of gradients of local batches is equivalent to an average of the gradients of all the samples in the large batch, which is exactly what happens in standard SGD training. The only thing that breaks the equivalence are the local data-dependent transformations such as batch normalization. The batch normalization is performed over each local batch separately instead of over the entire large batch combined.
Being the more radical approach, means that Federated Learning encounters some unique challenges. Perhaps the most crucial one concerns the distribution of data among the edge devices. For Federated Learning to achieve good performance, the classes distribution needs to be as similar as possible across the devices. For highly uneven, non-IID distributions of the local datasets (a rather common situation), Federated Learning performance deteriorates.

Federated learning has a hard time handling batches that are unevenly distributed
Large Batch, in comparison, is far better equipped to handle data which is non IID distributed: The averaging of the gradient over the local batches smoothes out the distribution. The large averaged batches are IID, or at least more so than the small local ones.
With this and the other challenges that Federated Learning brings with it, running independent multi-stage training has the clear, direct advantage of requiring fewer client-server communications. Fewer than in Large Batch training, that is, where communication has to occur constantly, with every batch. (On the other hand, being able to send out gradients instead of actual weights, does allow for some sparsity-based compression techniques to be applied.)
A Preliminary Empirical Comparison
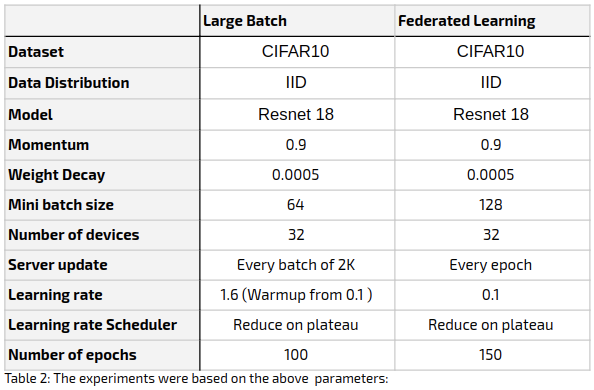
We have set out to benchmark the two approaches, pinning them against each other and against classical, single-server training. Our basic comparative philosophy was to run each methodology according to its own fitting or “standard” parameters, to the extent that this is possible. Large Batch requires comparably larger learning rates, for example, and so simply using the same parameters across all methodologies wouldn’t do. On the other hand, for the by-epoch comparison to make any kind of sense, we had to keep some uniformity. Importantly, as using momentum didn’t fit our optimization of the Federated Learning run, we had to avoid using momentum for the centralised and Large Batch training as well.
The experiment settings were as follows:
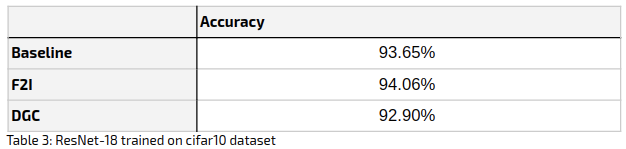
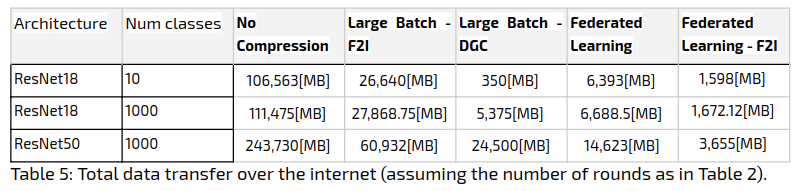
Dataset: CIFAR10, a relatively small, widely used benchmarking dataset. The 60K data points were split into a training set of 50K and a testing set of 10K data points. (We will present experiments on more substantial datasets in future posts.)
Architecture: Resnet18 (a common deep learning architecture).
Training was done from scratch (no pre-training).
Optimizer: SGD
Distributed setting: The training process was distributed across 96 virtual CPUs (with Intel Skylake inside). The training data for this experiment (before we get to post 3) was distributed in an even (IID) fashion.

Table 1: The parameters of the different methods
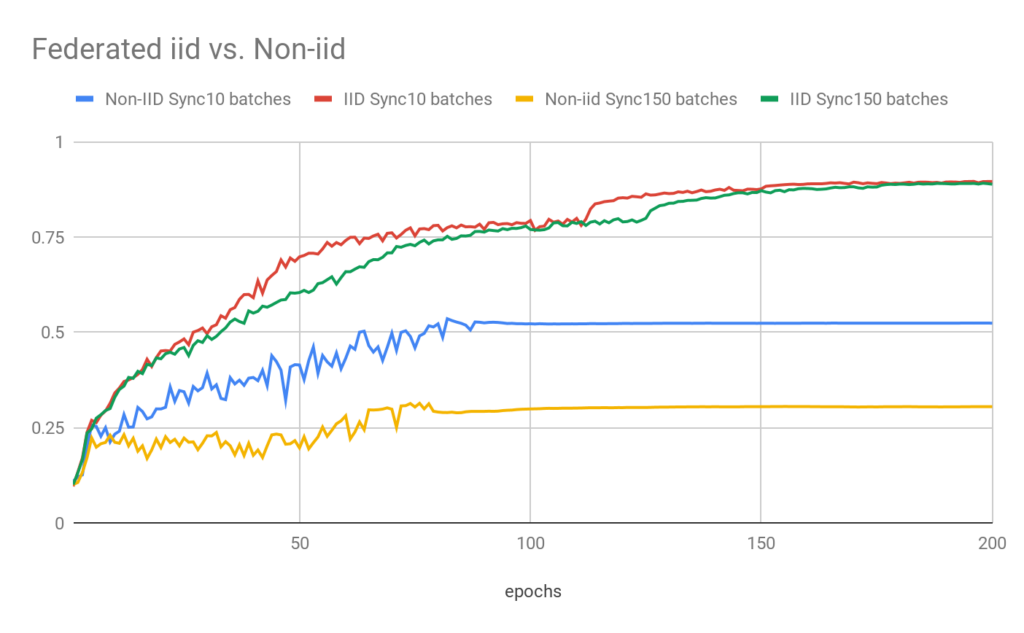
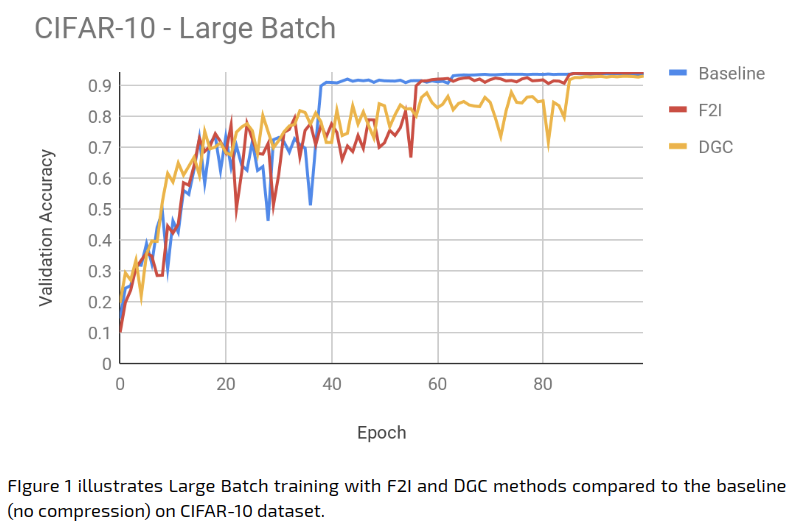
The experiment results were as follows (figure 1):
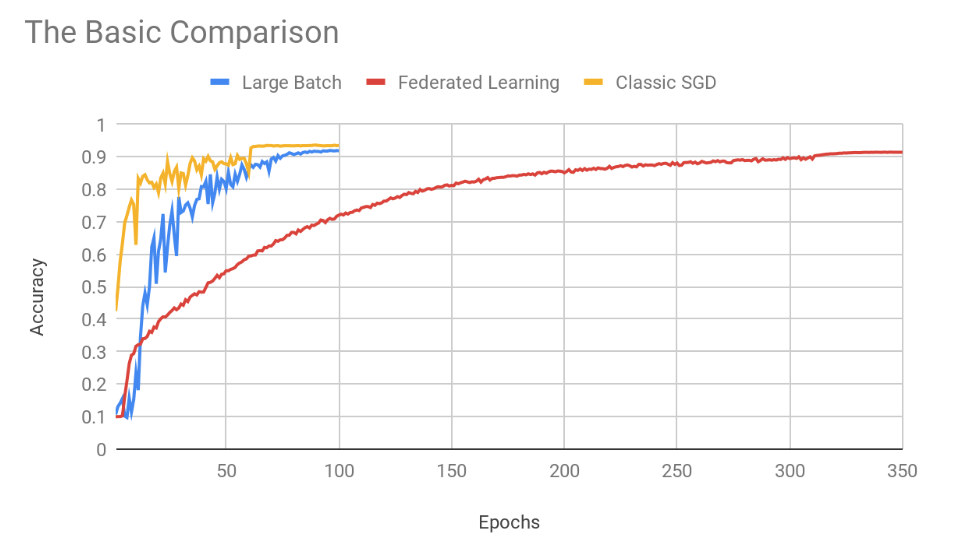
Figure 1: A graph of the three compared approaches — Large Batch, Federated Learning, and the classic single-server SGD training.
Using larger batches can slow convergence, as can more “extreme federating” of the training (synchronising once every more training rounds). In more challenging settings these can certainly also hurt or even destroy the final accuracy, though in the experiment above both distributed approaches managed to come close to the accuracy level of standard centralised training — ultimately. But as for speed, purely in terms of the epochs (i.e. passes on the data), the classical centralised approach indeed came out the fastest (with Federated Learning a far third).
Convergence by number of epochs, however, is in itself beside the point. The settings we are interested in are distributed to begin with. In those, training time is not simply computation time, but can be critically constrained by the communication cost. That, in turn, is intimately tied to the number of communication rounds. And after all, this was the point of developing Federated Learning over the more-standard Large Batch distribution. How do these two approaches compare in that fundamental respect, then? Here is a summary of the number of rounds required for reaching 80% accuracy in the experiment above:

Table 2: Number of communication rounds required during the training in order to reach an accuracy of 80% in the experiment as above. For Federated Learning, synched once every epoch, this is simply the number of epochs for 80% accuracy. For Large Batch, this is the number of epochs for 80% accuracy, times the number of (3072) batches that go into a single epoch (of 50,000 samples).
Conclusion
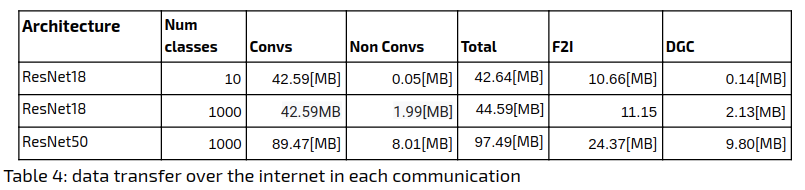
Distributing the training among many edge devices provides groundbreaking advantages. It also means, however, that communication cost now becomes an important factor, which has to be taken into account and managed, somehow. The number of rounds is but one fundamental aspect of it. The other side of the coin is the amount of data that has to be sent each time. This is the topic of our next post.
For now, to end on a very general note:
Our research, as we present here and in future posts, shows that there is no clear winner between the federated learning and Large batch approaches. Each has its pros and cons, depending mainly on the particulars of the use cases. Federated learning proves better for applications where connectivity is scarce and data is distributed uniformly (IID), whereas Large Batch fits better when data is distributed unevenly (Non IID) and communication is steady, and when we can gain value from high compression rates. Moreover, Federated Learning is only now beginning to be made to work for more complex problems such as the classification of Imagenet.
Our underlying recommendation is that researchers be proficient in both approaches and have the flexibility to choose between them according to the different use cases.